We can get the exponential function that defines the relationship between Uranium left and the time
The general formula for the exponential function is
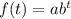
The scope of the question requires that we find the value of a and b in the function above
For the first data, when t=0, f(t)=100
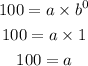
Thus
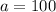
The next step will be to find b.
from the third data, when t=1, f(t)=25
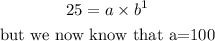
we will then solve for b
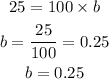
The final step will be to substitute the values of a and b into the formula
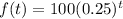
The final answer is option A