Question

There are 6 nickels and 7 dimes in your pocket. You randomly pick a coin out of your pocket and then return it to your pocket. Then you randomly pick another coin. What is the probability of you picking a nickel both times?

Answer 1

Given that;

There are 6 nickels and 7 dimes in your pocket.

Let N represent nickels and D represent dimes

Total coins will be

`6+7=13`

You randomly pick a coin out of your pocket and then return it to your pocket.

The probability of picking a nickel is

`P(N)=(6)/(13)`

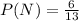
Since the coin was returned, the total number of coins is still the same

Then, you randomly pick another coin.

`P(N)=(6)/(13)`

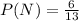
The probability of you picking a nickel both times will be

`\begin{gathered} P=P(N)* P(N) \\ P=(6)/(13)*(6)/(13)=(36)/(169) \end{gathered}`

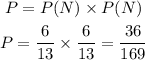
Hence, the answer is 36/169