Question

If using the method of completing the square to solve the quadratic equation x^2 + 15x + 21 = 0 which number would have been added to complete the square?

Answer 1

Step 1: Divide all terms by a (the coefficient of x2). In our case, it is 1. So it will not change anything.

Step 2: Move the number term (c/a) to the right side of the equation. In our case, it is 21. Therefore, we have:

`x^2\text{ + 15x = - 21}`

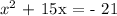
Step 3: Complete the square on the left side of the equation and balance this by adding the same value to the right side of the equation, this way:

`((15)/(2))^2=7.5^2\text{ = 56.25 }\Rightarrow x^2\text{ + 15x + 56.25 = -21 + 56.25}`

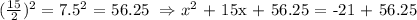
Step 4: Take the square root on both sides of the equation, as follows:

`\sqrt{(x^2\text{ + 15x + 56.25 }}=\text{ }√(35.25)`
`x\text{ + 7.5 = +/- 5.937}`

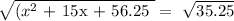
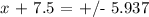
Step 5: Subtract the number that remains on the left side of the equation to find x, as follows:

`x\text{ = +/- 5.937 - 7.5 }\Rightarrow x_(1=+5.937-7.5=-1.563,)x_{2\text{ = -5.937 - 7.5 = - 13.437}}`

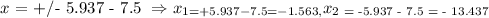
Now, we can asnwer the question, using the information from step 4 and 5:

56.25 would have been added to complete the square