Question

I can’t figure out the next no negative solution can you help?

Answer 1

x=0, x=1.772

Step-by-step explanation:

Given the equation:

`-5\cos ^2(x)+4\cos (x)+1=0`

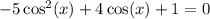
Let cos(x)=p

`\begin{gathered} -5\cos ^2(x)+4\cos (x)+1=0 \\ \implies-5p^2+4p+1=0 \end{gathered}`

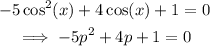
First, solve the equation above for p:

`\begin{gathered} -5p^2+5p-p+1=0 \\ -5p(p-1)-1(p-1)=0 \\ (-5p-1)(p-1)=0 \\ -5p-1=0\text{ or }p-1=0 \\ \implies p=-(1)/(5)\text{ or }p=1 \end{gathered}`

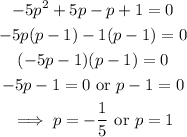
Recall that we made the substitution: cos(x)=p

When p=1

`\begin{gathered} \cos (x)=1 \\ x=\cos ^(-1)(1) \\ x=0 \end{gathered}`

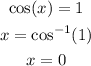
When p=-1/5

`\begin{gathered} \cos (x)=-(1)/(5) \\ x=\cos ^(-1)(-(1)/(5)) \\ x=1.772\text{ (in radians)} \end{gathered}`

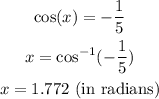
The smallest non-negative solutions to the equation are 0 and 1.772.