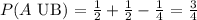Question

Find the indicated probability. Round your answer to 6 decimal places when necessary.Two "fair" coin are tossed. Let A be the event of number of heads equal 1 and B be the event of getting tails for the second coin.Find the probability that either A or B occurs

Answer 1

`P(A\text{ U B) = }(3)/(4)`

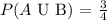
Step-by-step explanation:

Here, we want to find the probaility that either of two events occur

When we toss two coins at the same time, the possible results are:

`HT\text{ HH TH TT}`

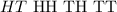
So, the first event is that we have a head only

We can see this in two out of the four and that makes its probability 2/4 = 1/2

The second event talks about getting tails in the second toss

We can see this in HT and TT too

The probability is 2/4 = 1/2

So, the probability that either occurs is the sum of the two which we have as follows:

`P(A\text{ U B) = P(A) + P(B) - P(A n B)}`

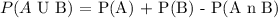
Now, the probability of P(A n B) is the intersection of the two sets

The intersection means that we have situations where we have one head, and we have tails in the second event

This situation arise in HT (one head and second coin tail)

The probability of this is 1/4 (1 out of 4)

Finally, we compute the probability of either or as follows:

`P(A\text{ UB) = }(1)/(2)+(1)/(2)-(1)/(4)\text{ = }(3)/(4)`