Question

Skill BuildeWatch the video and then solve the problem given below.Click here to watch the videoMargaret drove to a business appointment at 40 mph. Her average speed on the return trip was 30 mph. The return trip took 1/3 hour longer because of heavy traffic. How far did she travel to theappointment?She traveled milesEnter your answer in the answer box and then click Check Answer.All parts showing

Answer 1

Let's call the distance to the appointment 'd', and the time of the first travel (going to the appointment) 't'.

Now, we need to use the formula for the distance:

`\text{distance}=\text{average speed }\cdot\text{ time}`

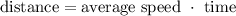
For the first part of the trip, we have the distance 'd', the average speed is 40 mph and the time is 't':

`d=40\cdot t`

Then, for the second part of the trip (return trip), the distance is also 'd', the average speed is 30 mph, and the time is 't + 1/3', because she took 1/3 hour longer than the first trip.

So we have that:

`d=30\cdot(t+(1)/(3))=30t+10`

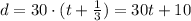
Now, we just need to equate both 'd':

`\begin{gathered} 40t=30t+10 \\ 10t=10 \\ t=1 \end{gathered}`

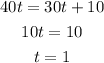
So the time 't' is 1 hour. Now we can use that to find the distance 'd':

`d=40t=40\cdot1=40`

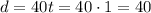
So the distance to the appointment is 40 miles.