Question

For each of the above sets of sample data calculate the coefficient of variation CV round to one decimal place

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the formula for calculating coeffieicient of Variation

`CV=\frac{standard\text{ }deviation}{mean}\cdot100`

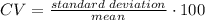
STEP 2: Find the coeffieicient of Variation for sample A

Find the standard deviation of sample A

The data set of Sample A are given as:

`36900,19400,22000,21900,35300,20500,35400,24000,37700,35300,38300,29600,26000,38400`

The standard deviation of the sample data is:

`7421.56421`

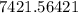
The mean is given as:

`30050`

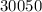
The coefficient of Variation will be:

`\begin{gathered} (7421.56421)/(30050)\cdot100=24.69738 \\ \\ \approx24.7\% \end{gathered}`

Hence, the coefficient of Variation for sample data A is approximately 24.7%

STEP 3: Calculate for Data Sample B

Similarly, the standard deviation of the given set of data will be:

`1.09486`

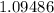
The mean is given as:

`3.24545`

The coefficient of Variation will be:

`\begin{gathered} (1.09486)/(3.24545)\cdot100=33.73522 \\ \\ \approx33.7\% \end{gathered}`

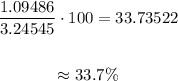
Hence, the coefficient of Variation for data set B is approximately 33.7%