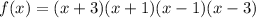ANSWER :
A. (-3, 0) multiplicity 1, (-1, 0) multiplicity 1, (1, 0) multiplicity 1 and (3, 0) multiplicity 1.
B. Domain : (-∞, ∞)
C. Range : (-16, ∞)
D. Degree : 4
E. f(x) = (x + 3)(x + 1)(x - 1)(x - 3)
EXPLANATION :
From the problem, we have a graph in the illustration.
A. Roots are the points in which the graph intersects the x-axis.
Multiplicity means how many times the graph intersects at the specific point.
Roots :
The graph intersects at (-3, 0) multiplicity 1, (-1, 0) multiplicity 1, (1, 0) multiplicity 1 and (3, 0) multiplicity 1.
B. Domain and Range.
Domain is the set of x-values in the graph.
Range is the set of y-values in the graph.
From the graph,
Domain :
x values are all real numbers. (-∞, ∞)
Range :
y values are from y = -16 to the positive infinity. That will be (-16, ∞)
C. Degree : 4
D. The equation of a function with a degree of 4 is given by :
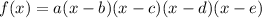
where a = coefficient
b, c, d and e are the roots of the function.
Since we already solved for the roots, that will be :
b = -3, c = -1, d = 1 and e = 3
The equation will be :
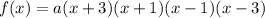
Plug in the given point (0, 9) then solve for the value of "a"
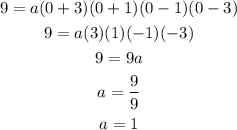
The equation will be :