Given:
The rate of change in volume = 12 cubic feet per minute.
We need to find the rate of change of radius at radius = 6 feet.
Consider the formula to find the volume of the sphere.
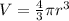
Differentiate with respect to t.
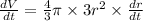
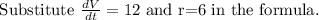
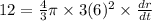
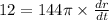
Dividing both sides by 144pi, we get
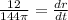
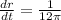
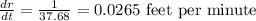
Hence the radius of the balloon increases by 0.03 feet per minute.