Question

In triangle ABC, the segments drawn from the vertices intersect at point G. Segment FG measures 6 cm, and segment FC measures 18 cm. Which best explains whether point G can be the centroid? (are the answers given here right? cos I'm not quite sure)

Answer 1

A centroid divides each median in a ratio 2:1, in this case, the segment FC is the sum of the segments FG and GC:

`FC=FG+GC`

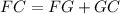
By solving for GC, we get:

`GC=FC-FG=18-6=12`

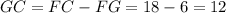
Then, the part of the median that goes from C to G has a length of 12 and the part that goes from the centroid to F has a length of 6, then we can express their ratio as 12:6, which is equivalent to 2:1.

Then the answer is:

Point G can be the centroid because 12:6 equals 2:1