The expresion for the correlation coefficient is :
![r=\frac{n\Sigma xy-\Sigma x\Sigma y}{\sqrt[]{\mleft\lbrace n\Sigma x^2-(\Sigma x)^2\}\mleft\lbrace n\Sigma y^2-(\Sigma y)\mright?^2\mright\rbrace}}](https://img.qammunity.org/2023/formulas/mathematics/college/2cfm1d9bw5izy80h3mmklc9as34wr68u00.png)
summation of x = 5 + 7 + 10 + 15 + 19
Summation of x = 56
Summation of y = 19 + 17 + 16 + 12 + 7
Summation of y = 71
Summation of prodcut xy
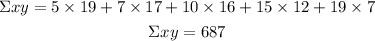
Summation of x^2 = 25 + 49 + 100 + 225 + 361
Summation of x^2 = 760
Summation of y^2 = 361 + 289 + 256 + 144 + 49
Summation of y^2 = 1099
Substitute tha value in the expression of correlation coefficient
![\begin{gathered} r=\frac{n\Sigma xy-\Sigma x\Sigma y}{\sqrt[]{\mleft\lbrace n\Sigma x^2-(\Sigma x)^2\}\mleft\lbrace n\Sigma y^2-(\Sigma y)\mright?^2\mright\rbrace}} \\ r=\frac{5(687)-56*71}{\sqrt[]{\mleft\lbrace5(760)-(56)^2\}\mleft\lbrace5(1099\mright)-(71\mright)^2}} \\ r=\frac{541}{\sqrt[]{\begin{cases}3800-3136\}\mleft\lbrace5495-5042\mright\rbrace\end{cases}}} \\ r=\frac{541}{\sqrt[]{300792}} \\ r=(541)/(548.44) \\ r=0.985 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/atx3c5ojzli0gurfydun0alqbdyklzdqev.png)
Answer: A) Correlation coefficient is 0.985