Question

What is the actual distance between these two cities in kilometers?

Answer 1

`70km`

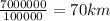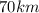
1) Whenever we have problems that deal with the real distance and distance on the map, we can write out the following formula:

`\begin{gathered} Scale=(distance\: on\: the \: map)/(real\: distance) \\ S=(3.5)/(R) \end{gathered}`

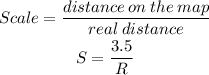
So, let's call the Real distance "R". Note that in this question, 1 centimeter represents 20 kilometers

2) So, in order to plug that as the scale we need to convert kilometers to centimeters:

`\begin{gathered} 1km--100000cm \\ 20km---x \\ x=2000000cm \end{gathered}`

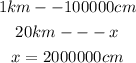
3) Finally, we can plug that into the formula and cross multiply the ratios this way:

`\begin{gathered} (3.5)/(r)=(1)/(2000000) \\ r=2000000*3.5 \\ r=7000000cm \end{gathered}`

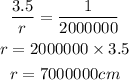
Converting it back to kilometers we can write:

`(7000000)/(100000)=70km`