Answer:
After solving the inequality, we get:
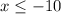
With the plotted inequality given.
Explanation:
Step 1: Manipulate and solve the inequality
The inequality is given as:
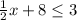
Make
 the subject of the inequality to solve it:
the subject of the inequality to solve it:
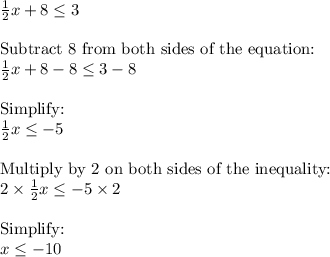
Step 2: Plot the inequality
After solving the inequality, we get:
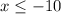
Which means that
 consists of all values that are equal to and less than
consists of all values that are equal to and less than
 .
.
On a number line, when the inequality includes the value, it is denoted by a closed circle.
With all this information, let's plot the number line: