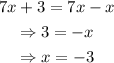Question

given the equation 7x + 3 = 7X - _______ , what's would go in the blank to make each of the following true:so the equation is true for no values of xso the equation is true for all values of xso the equation is true for only one value of x

Answer 1

Let k be the number in the blank, so that:

`7x+3=7x-k`

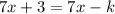
Substract 7x from both sides:

`3=-k`

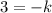
These two equations are equivalent regardless the value of x. We can change the conclusions that we may obtain by choosing different values for k.

Then, the equation:

`7x+3=7x-0`

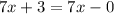
Is true for no values of x.

If we want the equation to be false regardless of the value of x, then set k so that -k is different from 3. For example, set k=0:

`\begin{gathered} 3=-0 \\ \Rightarrow3=0 \end{gathered}`

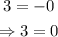
Since this is contradictory, then there are no values of x that make the equation true.

If we want the equation to be true for all values of x, then 3=-k must be an identity. Then, let k=-3:

`\begin{gathered} 3=-(-3) \\ \Rightarrow3=3 \end{gathered}`

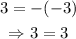
Then, the equation:

`7x+3=7x-(-3)`

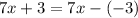
Is true for all values of x.

If we want the equation to be true for only one value of x, we have to bring back x into the equation 3=-k. So, we can take k=x. This way, we would have:

`\begin{gathered} 7x+3=7x-x \\ \Rightarrow3=-x \\ \Rightarrow x=-3 \end{gathered}`