Question

Find the turning point of y=h(x) if h(x)=f(-x)f(x)=x^2-4x+12

Answer 1

Given:

`y=h(x)\text{ where }h(x)=f(-x)\text{ and }f(x)=x^2-4x+12.`

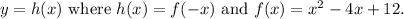
Required:

We need to find the turning point of y=h(x).

Step-by-step explanation:

Replace x =-x in the function f(x) to find h(x).

`f(-x)=(-x)^2-4(-x)+12.`
`f(-x)=x^2+4x+12.`

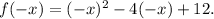
Replace f(-x)=y in the equation.

`y=x^2+4x+12.`
`y=x^2+2*2x+4+8.`
`y=x^2+2*2x+2^2+8.`
`Use\text{ }(a^2+2ab+b^2)=(a+b)^2.`
`y=(x+2)^2+8.`

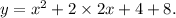
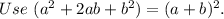
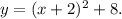
Which is of the form

`y=a(x-h)^2+k.`

where a=1, h=-2, and k=8.

The point (h,k)=(-2,8) is the turning point.

Final answer:

The turning point of y=h(x) is (-2,8).