To determine the arc length of the shaded area you have to use the following formula:
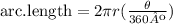
"θ" represents the measure of the central angle, in degrees
"r" represents the radius of the circle
We know that the arc measure is 126º, the central angle has the same measure as the intercepted arc, then its measure is also θ=126º
The radius of the circle is r=15cm
![\begin{gathered} \text{arc.length}=2\pi\cdot15\cdot((126)/(360)) \\ \text{arc.length}=30\pi\cdot(7)/(20) \\ \text{arc.length=}(21)/(2)\pi \\ \text{arclength}\approx32.98\approx33\operatorname{cm} \end{gathered}]()