Question

Diagram 10 shows a straight line PQ with point P(-4,9) and Q(12,1).

Answer 1

We have a line defined by two points, P(-4,9) and Q(12,1).

Knowing two points of the line, we can calculate the slope with the formula:

`m=(y_2-y_1)/(x_2-x_1)`

In this case, the slope will be:

`\begin{gathered} m=(y_Q-y_P)/(x_Q-x_P) \\ m=(1-9)/(12-(-4))=(-8)/(12+4)=-(8)/(16)=-(1)/(2) \end{gathered}`

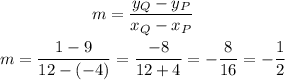
With the slope and one point we can express the equation in slope-point form:

`\begin{gathered} y-y_0=m(x-x_0) \\ y-y_Q=m(x-x_Q) \\ y-1=-(1)/(2)(x-12) \\ y=-(1)/(2)x+(12\cdot1)/(2)+1 \\ y=-(1)/(2)x+6+1 \\ y=-(1)/(2)x+7 \end{gathered}`

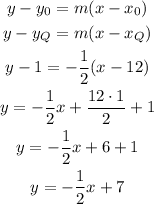
The x-intercept is the value of x that makes the function f(x) become 0.

In this case, we have to find x so that y = 0.

We can replace y in the equation and calculate x as:

`\begin{gathered} y=0 \\ -(1)/(2)x+7=0 \\ -(1)/(2)x=-7 \\ x=-7\cdot(-2) \\ x=14 \end{gathered}`

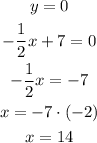
Then, for the x-intercept is x = 14.

Answer:

a) The equation of the line is y = (-1/2)*x+7

b) The x-intercept is x = 14.