SOLUTION
Given the question in the question tab, the following are the solution steps to answer the question.
STEP 1: Define an equation with one solution
You can tell that an equation has one solution if you solve the equation and get a variable equal to a number. A system of linear equations has one solution when the graphs intersect at a point.
STEP 2: Examine the options
An equation is said to have "no solution" when the coefficients are the same and the constants are different as seen below:
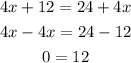
When the coefficients are the same and the constants are the same, the equation is said to have "infinitely many solutions as seen below:
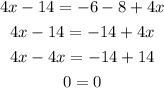
When the coefficients are different, the equation is said to have one solution as seen below:
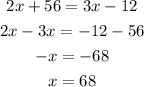
Hence, the answer is:
"When the coefficients are different"