Given:
![(9)/(8)\sqrt[8]{x}](https://img.qammunity.org/2023/formulas/mathematics/college/kckn5vo3lej0dvk2rva6p0d6sbqdqaunwq.png)
You can find the antiderivative by integrating it:
1. Set up:
![\int(9)/(8)\sqrt[8]{x}\text{ }dx](https://img.qammunity.org/2023/formulas/mathematics/college/cgvugatlqi169gev6pcafab4uqeuvw6m18.png)
2. You can rewrite it in this form:
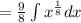
3. Apply this Integration Rule:
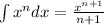
Then, you get:
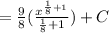
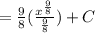
4. Simplify:
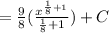
![=(9)/(8)(\frac{8\sqrt[8]{x^9}}{9})+C](https://img.qammunity.org/2023/formulas/mathematics/college/paxc6182k3t1sw4rtra8smzerz0f4xl93y.png)
![=\sqrt[8]{x^9}+C](https://img.qammunity.org/2023/formulas/mathematics/college/aijhzp5ae2qwm881mo47f6jndu0wht49q2.png)
Remember this Property for Radicals:
![\sqrt[m]{b^n}=b^{(n)/(m)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/i2kf8mowumt2ho4np6tw3rax2mls5r0wak.png)
You can rewrite the expression in this form:
![=\sqrt[8]{x\cdot x^8}+C](https://img.qammunity.org/2023/formulas/mathematics/college/g2znnx2eodsx35hhmzt063xfltxr3s7j1u.png)
Applying this Property for Radicals:
![\sqrt[n]{b^n}=b](https://img.qammunity.org/2023/formulas/mathematics/college/qrubqb7fdg6o0e5cfoz08o38dwzyw0xkzu.png)
You get:
![=x\sqrt[8]{x}+C](https://img.qammunity.org/2023/formulas/mathematics/college/yokx0mnrroa4ja68a5jbp4pc3gslxehwy9.png)
5. Knowing that:
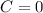
You obtain:
![=x\sqrt[8]{x}](https://img.qammunity.org/2023/formulas/mathematics/college/8io4vyi19efnjwjn1r7m78fxz945tteyop.png)
Hence, the answer is:
![=x\sqrt[8]{x}](https://img.qammunity.org/2023/formulas/mathematics/college/8io4vyi19efnjwjn1r7m78fxz945tteyop.png)