For the given functions, we will find the first derivative of each function
Note:
a, and b are constants
y, f, and g are functions
2) y = (a+bf)/g
We will use the quotient rule to find y' as follows:
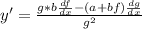
=============================================================
3) y = (x+f)/g
We will use the quotient rule to find y' as follows:
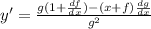
==========================================================
4) y = (x+f)³
We will use the exponent rule to find the derivative as follows:
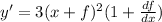
===========================================================
5) y = ax² + bg² + f
so, y' will be as follows:
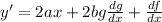
==========================================================