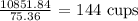SOLUTION.
The barrel and the cub are both cylinders. To find how many cups that will fill the barrel, we find the volumes of both the cup and the barrel and divide that of the barrel by the cup
Volume of a cylinder is given as

Volume of the cub becomes
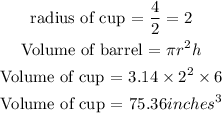
Number of cups become