Question

which of the following are point-slope equations of the line going through (-2,-2) and (2,1) check all that apply

Answer 1

The Point-Slope form of the equation of a line is:

`y_{}-y_1=m(x-x_1)_{}`

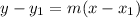
Where "m" is the slope of the line and this is a point on the line:

`(x_1,y_1)`

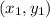
You can find the slope of a line using this formula:

`m=(y_2-y_1)/(x_2-x_1)`

In this case, knowing that this line passes through these points:

`(-2,-2);\mleft(2,1\mright)`

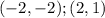
You can set up that:

`\begin{gathered} y_2=-2 \\ y_1=1 \\ x_2=-2 \\ x_1=2 \end{gathered}`

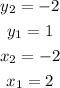
Substituting values into the formula and evaluating, you get:

`m=(-2-1)/(-2-2)=(-3)/(-4)=(3)/(4)`

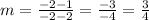
Knowing the slope and coordinates of two points on the line, you can set up these two equations for this line:

1. First equation:

`\begin{gathered} y-(-2)=(3)/(4)(x-(-2)) \\ \\ y+2=(3)/(4)(x+2) \end{gathered}`

2. Second equation:

`y-1=(3)/(4)(x-2)`

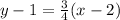
The answers are: Option A and Option B.