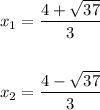Question

Find all the values of x where the tangent line is horizontal.3f(x) = x³ - 4x² - 7x + 12X=(Use a comma to separate answers as needed. Type an exact answer, using radicals

Answer 1

Given the function:

`h(x)=x^3-4x^2-7x+12`

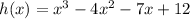
Find the first derivative:

`h^(\prime)(x)=3x^2-8x-7`

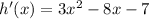
The first derivative gives us the slope of the tangent line to the graph of the function. When the tangent line is horizontal, the slope is 0, thus:

`3x^2-8x-7=0`

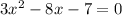
This is a quadratic equation with coefficients a = 3, b = -8, c = -7.

To calculate the solutions to the equation, we use the quadratic solver formula:

`$$x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}$$`

Substituting:

`x=(-(-8)\pm√((-8)^2-4(3)(-7)))/(2(3))`

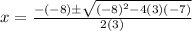
Operate:

`\begin{gathered} x=(8\pm√(64+84))/(6) \\ \\ x=(8\pm√(148))/(6) \end{gathered}`

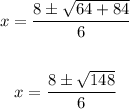
Since:

`148=2^2\cdot37`

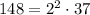
We have:

`\begin{gathered} x=(8\pm2√(37))/(6) \\ \\ \text{ Simplifying by 2:} \\ \\ x=(4\pm√(37))/(3) \end{gathered}`

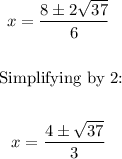
There are two solutions:

`\begin{gathered} x_1=(4+√(37))/(3) \\ \\ x_2=(4-√(37))/(3) \end{gathered}`