Question

how many cubic blocks with a side length of 1/6 cm are needed to fill the volume of this prism?The answer choices are 4,8,9,32.

Answer 1

Given the figure, we can deduce the following information:

Height=1/2 cm

Length=1/2 cm

Width= 1/6 cm

To determine the number of cubic blocks with a side length of 1/6 cm needed to fill the volume of the given prism, we first note that a cube has equal sides. So, the dimensions of the cube must be:

Height= 1/6 cm

Length=1/6 cm

Width=1/6 cm

Next, we get the volume of the cube by using the formula:

`\begin{gathered} Volume\text{ of the cube}=(Height)(Length)(Width) \\ =((1)/(6))((1)/(6))((1)/(6)) \\ Simplify \\ =(1)/(216)\text{ }cm^3\text{ } \end{gathered}`

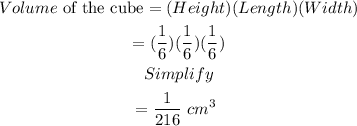
Then, we get the volume of the given prism using the same formula:

`\begin{gathered} Volume\text{ of the given prism}=(He\imaginaryI ght)(Length)(W\imaginaryI dth) \\ =((1)/(2))((1)/(2))((1)/(6)) \\ =(1)/(24)\text{ }cm^3\text{ } \end{gathered}`

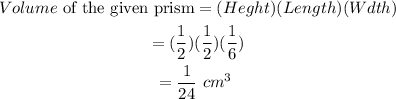
Now, we find the number cubic blocks by using the formula:

`\begin{gathered} Number\text{ }of\text{ cubic blocks}=\frac{Volume\text{ of the given prism}}{Volume\text{ of the cube}} \\ =((1)/(24))/((1)/(216)) \\ Simplify \\ =9 \end{gathered}`

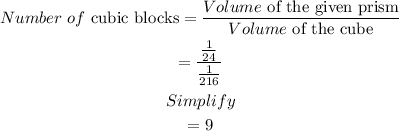
Therefore, the answer is 9.