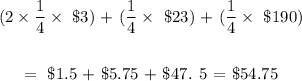Answer:
The fair price of the game is $54.75
The player is expected to win $54.75
Step-by-step explanation:
Here, we want to get the fair prize of the game
From the question, there are 4 prizes
When reaching into the box, we can only pick 1
Assuming that each of the prizes have the same probability oof being picked, the probability of picking any of the prize is 1/4
Now, to get the fair price of the game (it is obviously positive as we do not know if the player has anything to lose)
We have to multiply the probability by each of the price tag, then sum
Mathematically,we have this as: