Answer:
294 grams
Step-by-step explanation:
The amount of radioactive material left after t hours given that the half-life is to hours is
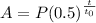
Now, in our case t0 = 3, t = 9 and P = 2352 g; therefore, the above equation gives
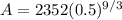
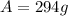
which is our answer!
Hence, the amount of radioactive copper left after 9 hours is 294 grams.