Given:

To Determine: The identity that is equivalent to the given tangent
Note that, the identity rule below would be applied
![\tan (\alpha)/(2)=\sqrt[]{(1-\cos \alpha)/(1+\cos \alpha)}](https://img.qammunity.org/2023/formulas/mathematics/college/599wetzl4q932ktzjbhg3ktoyia0u86zee.png)
Also,
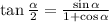
And also,
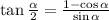
From the given tangent, we can re-write it as below:
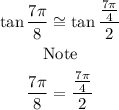
Therefore:
![\tan ((7\pi)/(4))/(2)=\sqrt[]{(1-\cos(7\pi)/(4))/(1+\cos(7\pi)/(4))}](https://img.qammunity.org/2023/formulas/mathematics/college/ac5gaj6b5okelelb8walna55w9z3n35u6q.png)
Also:
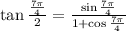
And also,
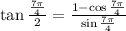
It can be observed from the option provided, the correct options is
I and III only