Quadratic formula
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Where a is the coefficient of the first term, b the coefficient of the second term and c the coefficient of third term
a)
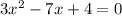
replacing on the quadratic formula
![x=\frac{-(-7)\pm\sqrt[]{(-7)^2-4(3)(4)}}{2(3)}](https://img.qammunity.org/2023/formulas/mathematics/college/mp895ch0ha5voyv19rsxp9d8vx8ichh9eq.png)
simplify
![\begin{gathered} x=\frac{7\pm\sqrt[]{49-48}}{6} \\ \\ x=\frac{7\pm\sqrt[]{1}}{6} \\ \\ x=(7\pm1)/(6) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/kkat1lyovbld51uawposyiq6wi52pd26tg.png)
x has two solutions
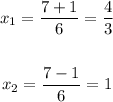
b)
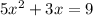
rewrite on general form
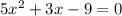
raplace on quadratic formula
![x=\frac{-(3)\pm\sqrt[]{(3)^2-4(5)(-9)}}{2(5)}](https://img.qammunity.org/2023/formulas/mathematics/college/vy8jfmoac39yfuhqmm09f368ogu1ungqmo.png)
simplify
![\begin{gathered} x=\frac{-3\pm\sqrt[]{9+180}}{10} \\ \\ x=\frac{-3\pm\sqrt[]{189}}{10} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/sncdyf2el3vlgjv2ax2kg1uq1w28sdk07g.png)
x has two solutions
![\begin{gathered} x_1=\frac{-3+\sqrt[]{189}}{10}\approx1.075 \\ \\ x_2=\frac{-3-\sqrt[]{189}}{10}\approx-1.67 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8s6qzz1uanw7omxftbnpem2dmw92ghvlhv.png)