Question

Round to the answer to the nearest tenth.18. A 24-foot ladder leaning against a building forms an 18° angle with the side of the building,How far is the base of the ladder from the base of the building?

Answer 1

In order to solve this problem, first let's draw the corresponding image to the problem:

Then, to calculate the distance x, we can use the sine relation of the angle of 18°.

The sine relation is the length of the opposite side to the angle over the length of the hypotenuse.

So we have:

`\begin{gathered} \sin (18\degree)=(x)/(24) \\ \text{0}.309=(x)/(24) \\ x=24\cdot0.309 \\ x=7.42 \end{gathered}`

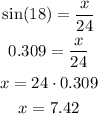
So the distance wanted is 7.42 ft.