Based on the given information, we can express the following
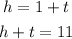
Because the digit of hundreds is 1 more the tens, and they sum 11. Let's combine the function to find t
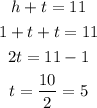
So, the digit of tens is 5.
Let's find the hundreds.
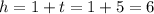
The number of hundreds is 6.
Hence, the number of blocks is 659.