Question

The owner of a video store has determined that the profits P of the store are approximately given by

Answer 1

The profit of the store is represented by the quadratic formula:

`P(x)=-x^2+90x+52`

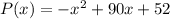
Where

P is the profit

x is the number of videos rented

The coefficients of the parabola are:

a= -1 (coefficient of the quadratic term)

b= 90 (coefficient of the x-term)

c=52 (constant)

The value of a is negative, which indicates that the parabola opens downwards and that its maximum value is represented by the vertex.

To determine the maximum profit, you have to determine the coordinates of the vertex.

First, calculate the x-coordinate of the vertex, to do so you have to use the following formula:

`x_v=-(b)/(2a)`

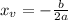
Replace it with the values of the coefficients a=-1 and b=90

`\begin{gathered} x_v=-(90)/(2\cdot(-1)) \\ x_v=-(90)/(-2) \\ x_v=45 \end{gathered}`

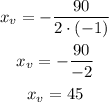
Second, replace x=45 in the equation to determine the y-coordinate of the vertex:

`\begin{gathered} y_v=P(45) \\ y_v=-(45^2)+90\cdot45+52 \\ y_v=-2025+4050+52 \\ y_v=2077 \end{gathered}`

The y-coordinate of the vertex represents the maximum profit.

So the maximum profit is $2077, the correct option is option A.