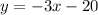Question

Find anequation for the perpendicular bisector of the line segment whose endpoints are(-8, 4) and (-4,-8).

Answer 1

to solve this question, we need to difine our variables

we have values for end points as

x1 = -8

y1 = 4

x2 = -4

y2 = -8

next we can find the slope of the equation

`\begin{gathered} \text{slope}=(y_2-y_1)/(x_2-x_1) \\ \text{slope}=(-8-4)/(-4-(-8)) \\ \text{slope}=(-12)/(4) \\ \text{slope}=-3 \end{gathered}`

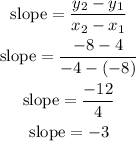
step 2

let's find the mid-point using mid-point formula

`\begin{gathered} md=(x_1+x_2)/(2),(y_2+y_1)/(2) \\ md=(-8+(-4))/(2),(-8+4)/(2) \\ md=-6,-2 \end{gathered}`

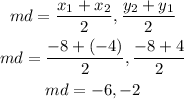
mid-point = (-6, -2)

now we know the perpendicular line travels (-6 , -2) and has a slope of -3

equation of a straight line => y = mx + c

we can solve for c to find the equation.

`\begin{gathered} y=mx+c \\ -2=(-3)(-6)+c \\ -2=18+c \\ c=-2-18 \\ c=-20 \end{gathered}`

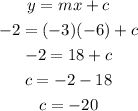
note: m = slope

c = intercept

the equation of the perpendicular bisector can be written as

y = -3x - 20

`y=-3x-20`