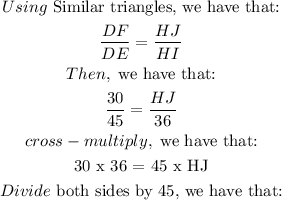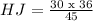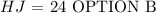Question

The following two right triangles are similar.If side DE = 45, side HI = 36, and side DF = 30, what is the length of side HJ?A)21B)24C)20D)19

Answer 1

Step 1:

In this question, we are given the following:

The following two right triangles are similar.If side DE = 45, side HI = 36, and side DF = 30, what is the length of side HJ?

Step 2:

The details of the solution are as follows:

Since side DE = 45, side HI = 36, and side DF = 30.

Then, the length of side HJ =

`\begin{gathered} Using\text{ Similar triangles, we have that:} \\ (DF)/(DE)=(HJ)/(HI) \\ Then,\text{ we have that:} \\ (30)/(45)=(HJ)/(36) \\ cross-multiply,\text{ we have that:} \\ 30\text{ x 36 = 45 x HJ} \\ Divide\text{ both sides by 45, we have that:} \end{gathered}`
`HJ=\frac{30\text{ x 36}}{45}`

`HJ\text{ = }(1080)/(45)`
`HJ\text{ = 24 \lparen OPTION B \rparen}`