Given:
4 5 6 7
Given that you picked a card at random, without replacement, you then pick a second card at random.
Let's find the probability of picking an even number and then picking an even number.
Number of possible events = 4
Number of even numbers = 4, 6, ==> 2 even numbers.
Hence, to find the probability, we have:
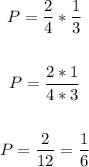
Therefore, the probability of picking an even number and then picking an even number is 1/6.
ANSWER:
