First solve for the hypotenuse of the given right triangle using the Pythagorean Theorem
![\begin{gathered} c^2=a^2+b^2 \\ c^2=6^2+8^2 \\ c^2=36+64 \\ c^2=100 \\ \sqrt[]{c^2}=\sqrt[]{100} \\ c=10 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/tfhn1shadljaxsud0m26bhc6kx31jhl468.png)
The hypotenuse is 10, we can now solve for the six trigonometric ratios.
Solving for the first three trigonometric ratios.
Recall the following ratios

Relative to angle Θ, we have the following sides
opposite = 8, adjacent = 6, hypotenuse = 10
Therefore, the ratio are the following

Solving for the reciprocal of the trigonometric ratios
Recall their reciprocal counterparts
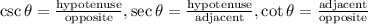
Substitute, and we have the following
