Question

The Jones family was one of the first to come to the U.S. They had 7 children. Assuming that the probability of a child being a girl is .5, find the probability that the Jones family had: At least 5 girls?At most 4 girls?

Answer 1

We will have the following:

First, we will remeber that:

`P(X=x)=\mleft(\begin{array}{c}n \\ x\end{array}\mright)p^xq^(n-x)`

Now, the probability of at least 5 girls will be:

`P(X\ge5)=P(X=5)+P(X=6)`
`\Rightarrow P(X\ge5)=\mleft(\begin{array}{c}7 \\ 5\end{array}\mright)(0.5)^5(0.5)^(7-5)+\mleft(\begin{array}{c}7 \\ 6\end{array}\mright)(0.5)^6(0.5)^(7-6)`
`\Rightarrow P(X\ge5)=((7!)/((7-5)!5!))(0.5)^5(0.5)^2+((7!)/((7-6)!6!))(0.5)^6(0.5)^1`
`\Rightarrow P(X\ge5)=(21)((1)/(32))((1)/(4))+(7)((1)/(64))(0.5)\Rightarrow P(X\ge5)=(21)/(128)+(7)/(128)`
`\Rightarrow P(X\ge5)=(7)/(32)\Rightarrow P(X\ge5)=0.21875`

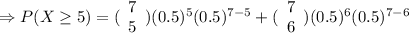
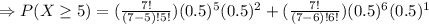
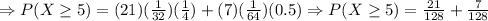
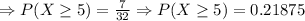
So, the probability of having at least 5 girls is 0.21875.

Now, the probability of having at most 4 girls will be:

`P(X\le4)=\sum ^4_(x=0)P(x)\Rightarrow P(X\le4)=P(0)+P(1)+P(2)+P(3)+P(4)`

So:

`P(X\le4)=\mleft(\begin{array}{c}7 \\ 0\end{array}\mright)(0.5)^0(0.5)^(7-0)+(\begin{array}{c}7 \\ 1\end{array})(0.5)^1(0.5)^(7-1)+(\begin{array}{c}7 \\ 2\end{array})(0.5)^2(0.5)^(7-2)+(\begin{array}{c}7 \\ 3\end{array})(0.5)^3(0.5)^(7-3)+(\begin{array}{c}7 \\ 4\end{array})(0.5)^4(0.5)^(7-4)`
`\Rightarrow P(X\le4)=(1)(1)((1)/(128))+(7)((1)/(2))((1)/(64))+(21)((1)/(4))((1)/(32))+(35)((1)/(8))((1)/(16))+(35)((1)/(16))((1)/(8))`
`\Rightarrow P(X\le4)=(1)/(128)+(7)/(128)+(21)/(128)+(35)/(128)+(35)/(128)\Rightarrow P(X\le4)=(99)/(128)`
`P(X\le4)=0.7734375`

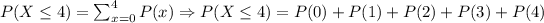
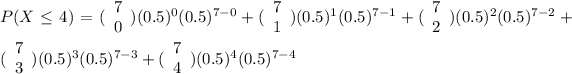
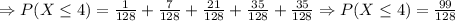
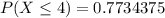
So, the probability of having at most 4 girls is 0.7734375.