The equation of a circle is given by the following general structure:

When solving the perfect squares we have:
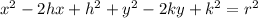
When looking at the given expression, we can observe that -18x and 12y are the equivalents for -2hx and -2ky. We can use this information to find h and k which are the coordinates of the center of the circle:
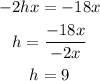
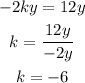
It means that the center of the circle is located at (9,-6).
To determine the radius of the circle, we have to take into account that 92 is the equivalent for h^2+k^2-r^2. Use this information to find r which is the radius of the circle:
![\begin{gathered} h^2+k^2-r^2=92 \\ 9^2+(-6)^2=92+r^2 \\ 81+36=92+r^2 \\ r^2=117-92 \\ r^2=25 \\ r=\sqrt[]{25} \\ r=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ouzjiwbozs3y3xg5tlxy633nz272e323vg.png)
It means that the radius of the circle is 5.