Step 1. Find the dimensions of the left-hand side of the equation.
In this part of the equation what we have is:
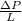
Here Δ represents a change in P, in the end, ΔP and P have the same units
And we are indicated that the units of P and L are:
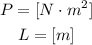
Note: we use [ ] to represent that they are units.
Thus in this left part of the equation, the units are:
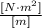
Simplifying the m:
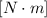
Step 2. We have found that the units on the left-hand side are N*m
Now, we have to find the units on the right-hand side.
On the right-hand side of the equation we have:
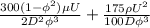
The units of the variables are:
![\begin{gathered} \phi=Dimensionless\text{ (no units)} \\ \mu=\lbrack Pa\cdot s\rbrack \\ U=\lbrack(m)/(s)\rbrack \\ D=\lbrack m\rbrack \\ \rho=\lbrack\frac{\operatorname{kg}}{m^3}\rbrack \end{gathered}]()
Substituting the units (we can ignore the numbers and the dimensionless terms):
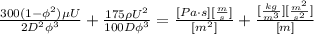
Simplifying the divisions and multiplications between the units:
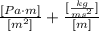
Simplifying further:
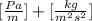
Since the units of Pascals can be also represented as:

The second term can also be expressed as Pa/m:
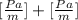
The addition of two terms with the same units does not change the units, thus, the units on the right-hand side are:
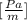
Step 3. Compare.
The units on the left-hand side are:
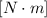
And the units on the right-hand side are:
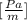
To compare them, let's convert the units of the left-hand side to Pascals using the following known relation between Newtons and Pascals:
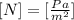
Using this, the units of the left-hand side are:
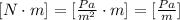
As you can see, The units of both sides are Pa/m, thus we have proven that the two sides are dimensionally consistent.