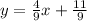Question

1 pt 51Find the equation (in terms of x) of the line through the points (-5,-1) and (4,3)y =

Answer 1

The line equation in slope-intercept form is given by

`y=\text{mx}+b`

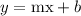
where m is the slope and b the y-intercept.

From the given points, we can find the slope m as follows,

`m=(y_2-y_1)/(x_2-x_1)`

where

`\begin{gathered} (x_1,y_1)=(-5,-1) \\ (x_2,y_2)=(4,3) \end{gathered}`

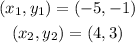
Then, by substituting these values into m, we have

`m=(3-(-1))/(4-(-5))`

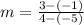
which gives

`m=(3+1)/(4+5)=(4)/(9)`

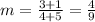
So, the line has the form

`y=(4)/(9)x+b`

In order to find b, we can substitute point (4,3) into the last result. It yields,

`3=(4)/(9)(4)+b`

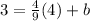
which gives

`\begin{gathered} 3=(16)/(9)+b \\ \text{then} \\ b=3-(16)/(9) \\ b=(27)/(9)-(16)/(9) \\ b=(11)/(9) \end{gathered}`

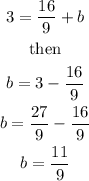
Therefore, the answer is:

`y=(4)/(9)x+(11)/(9)`