In the interval
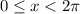
We have two values that sin is negative. I will draw a trigonometric circle:
We can find these values using a calculator.
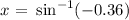
This will give -21.1 degrees. If we start counting from zero, one complete circle is 360 degrees. So to find x2 we have to do:
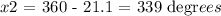
And to find x1 we have to add 21.1 degrees counting from the start that is now 180:
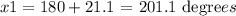
We do this process because we have two angles that give the same sin value, and they are symmetric compared to the sin axis!