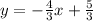Given:
Given line passes through (-1,3) and (5, -5).
Required: Equation of the line
Step-by-step explanation:
First, find the slope using the two point formula.
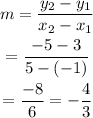
An equation of a line in slope-intercept form is y = mx+c, where m is the slope and c is the y-intercept.
Substitute the value of m into y = mx+c.
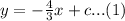
Plug the value (-1,3) into equation (1) to find c.
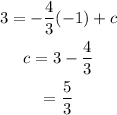
Substitute the obtained value of c into equation (1).
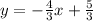
Final Answer: