ANSWER
$59
EXPLANATION
John's profit is represented by a quadratic function, whose leading coefficient is negative. This means that the graph is a parabola that opens downward and, therefore, the vertex is a maximum. In other words, the most profit he can earn is the y-coordinate of the vertex.
The x-coordinate of the vertex of a quadratic function given in standard form is,
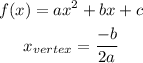
In this case, a = -1 and b = 10,
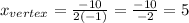
And the maximum profit is given by P(x_vertex),
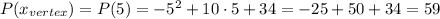
Hence, the most he can earn is $59.