Given the mass of the object, m= 8 kg.
Final speed of the object, v = 8 m/s
Initial speed of the object, u = 4 m/s
To find work done required to increase the speed from 4 m/s to 8 m/s
Work done = change in kinetic energy
Kinetic energy initially when speed is 4 m/s is given by
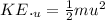
Substituting the values, initial kinetic energy will be
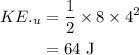
Similarly, final kinetic energy will be
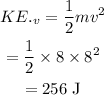
Work done will be
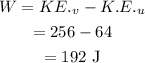
Thus, the required work done is 192 J.