According to the double-angle identity:
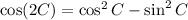
So, let's solve (a):
(a) Given:
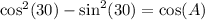
Comparing with the identity:
C = 30°
Then, 2C = 2*30 = 60°
Since
A = 2C, A = 60°
Answer: A = 60°.
(b) Given,
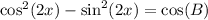
Comparing with the identity:
C = 2x
2C = 2*2x = 4x
Then,
B = 2C = 4x
Answer: B = 4x°.
In summary,
(a) A = 60°.
(b) B = 4x°.