Question

i am begging anyone to help me with this! (all tutors i've asked said they can't solve it but i need someone to help me out) - i can get the first little bit of it so maybe we can work through it together?

Answer 1

First, we need to calculate how much energy we will get from this combustion.

Assuming the combustion is complete, we have the octane reacting with O₂ to form only water and CO₂, so:

`C_8H_(18)+O_2\to CO_2+H_2O`

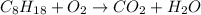
We need to balance the reaction. Carbon only appear on two parts, so, we can start by it:

`C_8H_(18)+O_2\to8CO_2+H_2O`

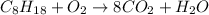
Now, we balance the hydrogen:

`C_8H_(18)+O_2\to8CO_2+9H_2O`

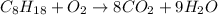
And in the end, the oxygen:

`C_8H_(18)+(25)/(2)O_2\to8CO_2+9H_2O`

We can multiply all coefficients by 2 to get integer ones:

`2C_8H_(18)+25O_2\to16CO_2+18H_2O`

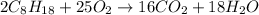
Now, we need to use the enthalpies of formation to get the enthalpy of reaction of this reaction.

The enthalpy of reaction can be calculated by adding the enthalpies of formation of the products multiplied by their stoichiometric coefficients and substracting the sum of enthalpies of formation of the reactants multiplied by their stoichiometric coefficients.

For the reactants, we have (the enthalpy of formation of pure compounds is zero, which is the case for O₂):

`\begin{gathered} \Delta H\mleft\lbrace reactants\mright\rbrace=2\cdot\Delta H\mleft\lbrace C_8H_(18)\mright\rbrace+25\cdot\Delta H\mleft\lbrace O_2\mright\rbrace \\ \Delta H\lbrace reactants\rbrace=2\cdot(-250.1kJ)+25\cdot0kJ \\ \Delta H\lbrace reactants\rbrace=-500.2kJ+0kJ \\ \Delta H\lbrace reactants\rbrace=-500.2kJ \end{gathered}`

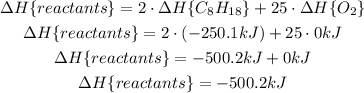
For the products, we have:

`\begin{gathered} \Delta H_{}\mleft\lbrace product\mright\rbrace=16\cdot\Delta H\lbrace CO_2\rbrace+18\cdot\Delta H\lbrace H_2O\rbrace \\ \Delta H_{}\lbrace product\rbrace=16\cdot(-393.5kJ)+18\cdot(-285.5kJ) \\ \Delta H_{}\lbrace product\rbrace=-6296kJ-5139kJ \\ \Delta H_{}\lbrace product\rbrace=-11435kJ \end{gathered}`

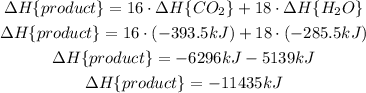
Now, we substract the rectants from the produtcs:

`\begin{gathered} \Delta H_r=\Delta H_{}\lbrace product\rbrace-\Delta H\lbrace reactants\rbrace \\ \Delta H_r=-11435kJ-(-500.2kJ) \\ \Delta H_r=-10934.8kJ \end{gathered}`

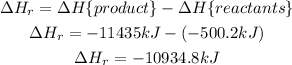
Now, this enthalpy of reaction is for 2 moles of C₈H₁₈, so for 1 mol of C₈H₁₈ we have half this value:

`\Delta H_c=(1)/(2)\Delta H_r=(1)/(2)\cdot(-10934.8kJ)=-5467.4kJ`

Now, we have 100 g of C₈H₁₈, and its molar weight is approximately 114.22852 g/mol, so the number of moles in 100 g of C₈H₁₈ is:

`\begin{gathered} M_{C_8H_(18)}=\frac{m_{C_8H_(18)}}{n_{C_8H_(18)}} \\ n_{C_8H_(18)}=\frac{m_{C_8H_(18)}}{M_{C_8H_(18)}}=(100g)/(114.22852g/mol)\approx0.875438mol \end{gathered}`

Since we have approximately 0.875438 mol, and 1 mol releases -5467.4kJ when combusted, we have:

`Q=-5467.4kJ/mol\cdot0.875438mol\approx-4786.37kJ`

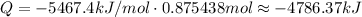
Now, for the other part, we need to calculate how much heat it is necessary to melt a mass, m.

First, we have to heat the ice to 0 °C, so:

`\begin{gathered} Q_1=m\cdot2.010J/g.\degree C\cdot(0-(-10))\degree C \\ Q_1=m\cdot2.010J/g\cdot10 \\ Q_1=m\cdot20.10J/g \end{gathered}`

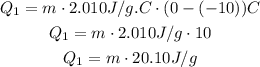
Then, we need to melt all this mass, so we use the latent heat now:

`Q_2=n\cdot6.03kJ/mol`

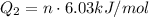
Converting mass to number of moles of water we have:

`\begin{gathered} M=(m)/(n) \\ n=(m)/(M)=(m)/(18.01528g/mol) \end{gathered}`

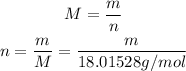
So:

`Q_2=(m)/(18.01528g/mol)_{}\cdot6.03kJ/mol\approx m\cdot0.334716kJ/g`

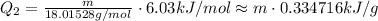
Adding them, we have a total heat of:

`\begin{gathered} Q_T=m\cdot20.10J/g+m\cdot0.334716kJ/g \\ Q_T=m\cdot0.02010kJ/g+m\cdot0.334716kJ/g \\ Q_T=m\cdot0.354816kJ/g \end{gathered}`

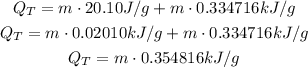
Since we have a heat of 4786.37 kJ form the combustion, we input that to get the mass (the negative sign is removed because it only means that the heat is released from the reaction, but now it is absorbed by the ice):

Since we have a total of 20kg of ice, we can clculate the percent using it: