Question

Which of the following are solutions to the following solutions to the following solutions?

Answer 1

We have to find the solutions to the equation:

`|x+4|=8`

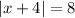
The absolute value function is in fact a piecewise function, so it may have two solutions.

We consider for the first solution that the argument inside the absolute function is positive, that is x + 4 > 0. Then, we will have:

`\begin{gathered} x+4=8 \\ x=8-4 \\ x=4 \end{gathered}`

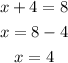
Now, we consider that the the argument is negative and is made positive by the absolute value function (it will shift the sign, which can be represented by a multiplication by -1). This means that x + 4 < 0, and the solution will be:

`\begin{gathered} -(x+4)=8 \\ -x-4=8 \\ -x=8+4 \\ -x=12 \\ x=-12 \end{gathered}`

We can see it in a graph as:

Answer: the solutions are x = 4 and x = -12.