ANSWER
1987 and 1995
Step-by-step explanation
The revenue is modeled by:
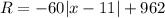
To find the years that the revenue was $722 million, we have to solve for x when R is 722.
That is:
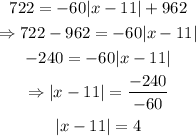
We can split the absolute value equation into two different equations because the term in the absolute value is equal to both the positive and the negative of the term on the other side of the equality.
That is:
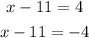
Solve for x in both:
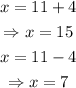
That is to say 7 and 15 years after 1980.
Therefore, in the years 1987 and 1995, the revenue was $722 million.