Question

Convert the equation of a parabola to vertex formy^2+4x-14y+57=0

Answer 1

`y^2+4x-14y+57=0`

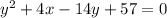
first we need to solve X

`\begin{gathered} -y^2+14y-57=4x \\ x=-(1)/(4)y^2+(7)/(2)y-(57)/(4) \\ \end{gathered}`

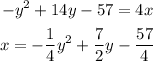
we need to write the equation on this form

`x=a(y-h)^2+k`

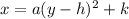
where h=-(b/2a) and k=c- a (b/2a)2

we obtain a,b and c from the equation to solve x

so a=-1/4, b=7/2 and c=-57/4

now lets find h and k

`\begin{gathered} h=-((b)/(2a)) \\ h=-(((7)/(2))/(2\cdot-(1)/(4))) \\ \\ h=-(((7)/(2))/((-1)/(2))) \\ \\ h=-(-7) \\ h=7 \end{gathered}`
`\begin{gathered} k=c-a((b)/(2a))^2 \\ \\ k=-(57)/(4)-(-(1)/(4))(((7)/(2))/(2\cdot-(1)/(4)))^2 \\ \\ k=-(57)/(4)+(1)/(4)(-7)^2 \\ \\ k=-(57)/(4)+(1)/(4)(49) \\ \\ k=-(8)/(4) \\ k=-2 \end{gathered}`

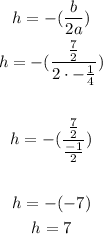
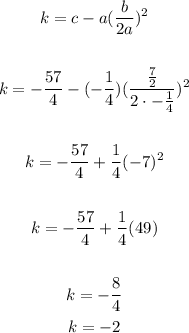
now replace a, h and k on the equation

`\begin{gathered} x=a(y-h)^2+k \\ \\ x=-(1)/(4)(y-7)^2-2 \end{gathered}`

the evrtex is (h,k)=(7,-2)