Let the angle be 'x' degrees.
The complement (C) of the corresponding angle will be,
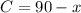
And the supplement (S) of the corresponding angle will be,
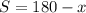
According to the condition given in the problem,
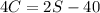
Substitute the values,
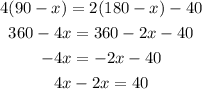
Simplify the expression further,
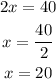
Substitute this value of 'x' to obtain the complement and supplement angles as follows,
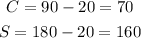
Thus, the angle measures 20 degrees, its complement measures 70 degrees, while its supplement measures 160 degrees.