Step-by-step explanation
The probability (P) is winning in less than four turns can be decomposed as the following sum:
The probability of winning in one turn is

The probability of winning in the second turn is
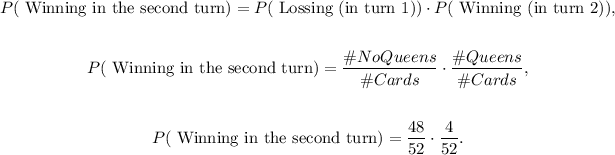
The probability of winning in the third turn is
![\begin{gathered} P(\text{ Winning in the third turn})=P(\text{ Lossing (in turn 1)})\cdot P(\text{ Lossing (in turn 2)})\cdot P(\text{ winning (in turn 3)}), \\ \\ P(\text{ Winning in the third turn})=(\#NoQueens)/(\#Cards)\cdot(\#NoQueens)/(\#Cards)\cdot(\#Queens)/(\#Cards), \\ \\ P(\text{ Winning in the third turn})=(48)/(52)\cdot(48)/(52)\cdot(4)/(52)\text{.} \end{gathered}]()
Adding all together, we get

Answer
The probability of winning in less than four turns is (approximately) 21.35%.